CorCTF2022 WriteUp

Last weekend, I played corCTF 2022 with Water Paddler. I’ll write up some of rev and crypto challenges.

tadpole

from Cryptodome.Util.number import bytes_to_long, isPrime
from secrets import randbelow

p = bytes_to_long(open("flag.txt", "rb").read())
assert isPrime(p)

a = randbelow(p)
b = randbelow(p)

def f(s):
    return (a * s + b) % p

print("a = ", a)
print("b = ", b)
print("f(31337) = ", f(31337))
print("f(f(31337)) = ", f(f(31337)))

Let’s define two variables first. $$ s_1 = f(31337) $$

$$ s_2 = f(s_1) $$

At first, I think I have to solve some congruence equations. That’s not necessary. The most efficient way to get a prime value is to use gcd() We can use gcd in this challenge as well. $$ a \cdot s_1 + b = s_2 + k_1 \cdot p $$

$$ a \cdot 31337 + b = s_1 + k_2 \cdot p $$

We can easily calculate p using gcd().

import math

from Cryptodome.Util.number import long_to_bytes

a =  7904681699700731398014734140051852539595806699214201704996640156917030632322659247608208994194840235514587046537148300460058962186080655943804500265088604049870276334033409850015651340974377752209566343260236095126079946537115705967909011471361527517536608234561184232228641232031445095605905800675590040729
b =  16276123569406561065481657801212560821090379741833362117064628294630146690975007397274564762071994252430611109538448562330994891595998956302505598671868738461167036849263008183930906881997588494441620076078667417828837239330797541019054284027314592321358909551790371565447129285494856611848340083448507929914
f1 =  52926479498929750044944450970022719277159248911867759992013481774911823190312079157541825423250020665153531167070545276398175787563829542933394906173782217836783565154742242903537987641141610732290449825336292689379131350316072955262065808081711030055841841406454441280215520187695501682433223390854051207100
f2 =  65547980822717919074991147621216627925232640728803041128894527143789172030203362875900831296779973655308791371486165705460914922484808659375299900737148358509883361622225046840011907835671004704947767016613458301891561318029714351016012481309583866288472491239769813776978841785764693181622804797533665463949

p = math.gcd(a * f1 + b - f2, a * 31337 + b - f1)

print(long_to_bytes(p))

luckyguess

from random import getrandbits

p = 2**521 - 1
a = getrandbits(521)
b = getrandbits(521)
print("a =", a)
print("b =", b)

try:
    x = int(input("enter your starting point: "))
    y = int(input("alright, what's your guess? "))
except:
    print("?")
    exit(-1)

r = getrandbits(20)
for _ in range(r):
    x = (x * a + b) % p

if x == y:
    print("wow, you are truly psychic! here, have a flag:", open("flag.txt").read())
else:
    print("sorry, you are not a true psychic... better luck next time")

The point here is we cannot know how many times it takes to calculate x. A simple idea is to find a fixed point. $$ x == (x \cdot a + b) \mod p $$

$$ (a - 1) \cdot x == -b \mod p $$

OK, now it’s easy to calculate x. This challenge didn’t require a strict timeout. I didn’t use pwntools to automate, just copy and paste :)

from icecream import ic
import gmpy2

p = gmpy2.mpz(2**521 - 1)
a = gmpy2.mpz(5416766863480819098182406178148169848510098381348133948161642906028099842277283941433099762924636386764834443323775473184924574805814771928372003099947515463)
b = gmpy2.mpz(2309171399245954414491797405618482884840044887825031267457661779887603870211578605597458941450182790451854883551150433109896403412847210053312353049604115651)

x = (gmpy2.invert(a - 1, p) * (p - b)) % p
assert x == (x * a + b) % p

print(x.digits())

exchanged

from Crypto.Util.number import *
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from hashlib import sha256
from secrets import randbelow

p = 142031099029600410074857132245225995042133907174773113428619183542435280521982827908693709967174895346639746117298434598064909317599742674575275028013832939859778024440938714958561951083471842387497181706195805000375824824688304388119038321175358608957437054475286727321806430701729130544065757189542110211847
a = randbelow(p)
b = randbelow(p)
s = randbelow(p)

print("p =", p)
print("a =", a)
print("b =", b)
print("s =", s)

a_priv = randbelow(p)
b_priv = randbelow(p)

def f(s):
    return (a * s + b) % p

def mult(s, n):
    for _ in range(n):
        s = f(s)
    return s

A = mult(s, a_priv)
B = mult(s, b_priv)

print("A =", A)
print("B =", B)

shared = mult(A, b_priv)
assert mult(B, a_priv) == shared

flag = open("flag.txt", "rb").read()
key = sha256(long_to_bytes(shared)).digest()[:16]
iv = long_to_bytes(randint(0, 2**128))
cipher = AES.new(key, AES.MODE_CBC, iv=iv)
print(iv.hex() + cipher.encrypt(pad(flag, 16)).hex())

The first strange thing is a_priv and b_priv are not small numbers. It is impossible for the author to naively iterate to calculate A and B.

$$ mult(s, n) = a ^ n \cdot s + b \cdot \sum_{i=0}^{n - 1} a^i \mod p $$

$$ mult(s, n) = a ^ n \cdot s + b \cdot \frac{a^n - 1}{a - 1} \mod p $$

$$ A = a^n \cdot s + b \cdot \frac{a^{n} - 1}{a - 1} \mod p $$

$$ (a - 1) \cdot A = (a - 1) \cdot s \cdot a ^ n + b \cdot (a ^ n - 1) \mod p $$

$$ (a \cdot s - s + b) \cdot a ^ n = (a - 1) \cdot A + b \mod p $$

Now, it’s easy to calculate $a^{a_{priv}}$ and $a^{b_{priv}}$ and shared.In my solution, I tried to calculate $a_{priv}$ directly using sagemath. It’s not mandatory, just fun.

p = 142031099029600410074857132245225995042133907174773113428619183542435280521982827908693709967174895346639746117298434598064909317599742674575275028013832939859778024440938714958561951083471842387497181706195805000375824824688304388119038321175358608957437054475286727321806430701729130544065757189542110211847
a = 118090659823726532118457015460393501353551257181901234830868805299366725758012165845638977878322282762929021570278435511082796994178870962500440332899721398426189888618654464380851733007647761349698218193871563040337609238025971961729401986114391957513108804134147523112841191971447906617102015540889276702905
b = 57950149871006152434673020146375196555892205626959676251724410016184935825712508121123309360222777559827093965468965268147720027647842492655071706063669328135127202250040935414836416360350924218462798003878266563205893267635176851677889275076622582116735064397099811275094311855310291134721254402338711815917
s = 35701581351111604654913348867007078339402691770410368133625030427202791057766853103510974089592411344065769957370802617378495161837442670157827768677411871042401500071366317439681461271483880858007469502453361706001973441902698612564888892738986839322028935932565866492285930239231621460094395437739108335763
A = 27055699502555282613679205402426727304359886337822675232856463708560598772666004663660052528328692282077165590259495090388216629240053397041429587052611133163886938471164829537589711598253115270161090086180001501227164925199272064309777701514693535680247097233110602308486009083412543129797852747444605837628
B = 132178320037112737009726468367471898242195923568158234871773607005424001152694338993978703689030147215843125095282272730052868843423659165019475476788785426513627877574198334376818205173785102362137159225281640301442638067549414775820844039938433118586793458501467811405967773962568614238426424346683176754273
def quick_multi(s, n):
    return Integer(mod(a, p) ^ n * s + (mod(a, p) ^ n - 1) / (mod(a, p) - 1) * b)
a_priv = discrete_log((b + mod(A, p) * (a - 1)) / (a * s - s + b), mod(a, p))
assert A == quick_multi(s, a_priv)
from Crypto .Util.number import long_to_bytes
from hashlib import sha256
shared = quick_multi(B, a_priv)
key = sha256(long_to_bytes(shared)).digest()[:16]
from Crypto.Cipher import AES
ciphertext = bytes.fromhex("e0364f9f55fc27fc46f3ab1dc9db48fa482eae28750eaba12f4f76091b099b01fdb64212f66caa6f366934c3b9929bad37997b3f9d071ce3c74d3e36acb26d6efc9caa2508ed023828583a236400d64e")
iv = ciphertext[:16]
cipher = AES.new(key, AES.MODE_CBC, iv=iv)
cipher.decrypt(ciphertext[16:])

Microsoft ❤️ Linux

This is a really fun challenge. The first strange thing is the name of attachment ends with exe. However, there is a ELF magic in the binary and it can run on my ArchLinux. Let’s take a look in Binary Ninja. The attachment can be downloaded here.

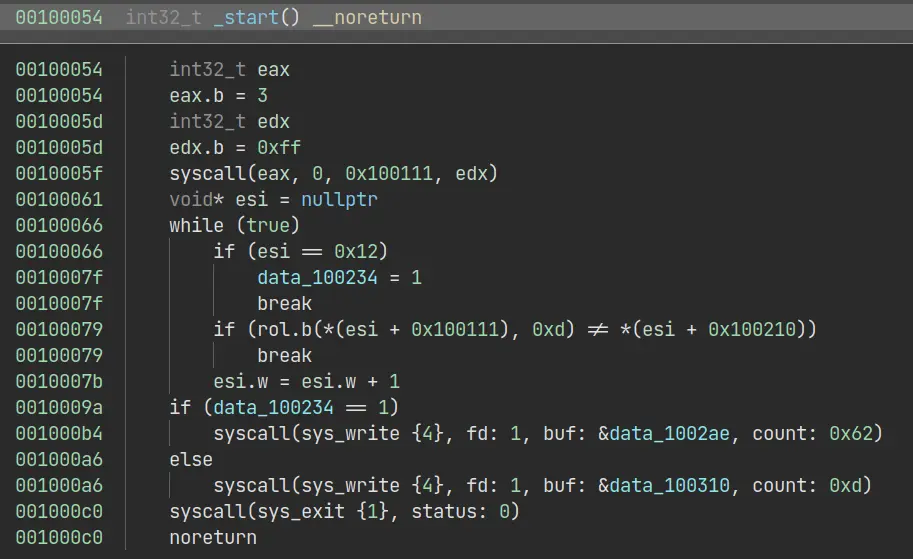
Binary Ninja screenshot

OK, this part is easy. Just rol and compare. We can easily get first part of the flag. The second part is interesting.

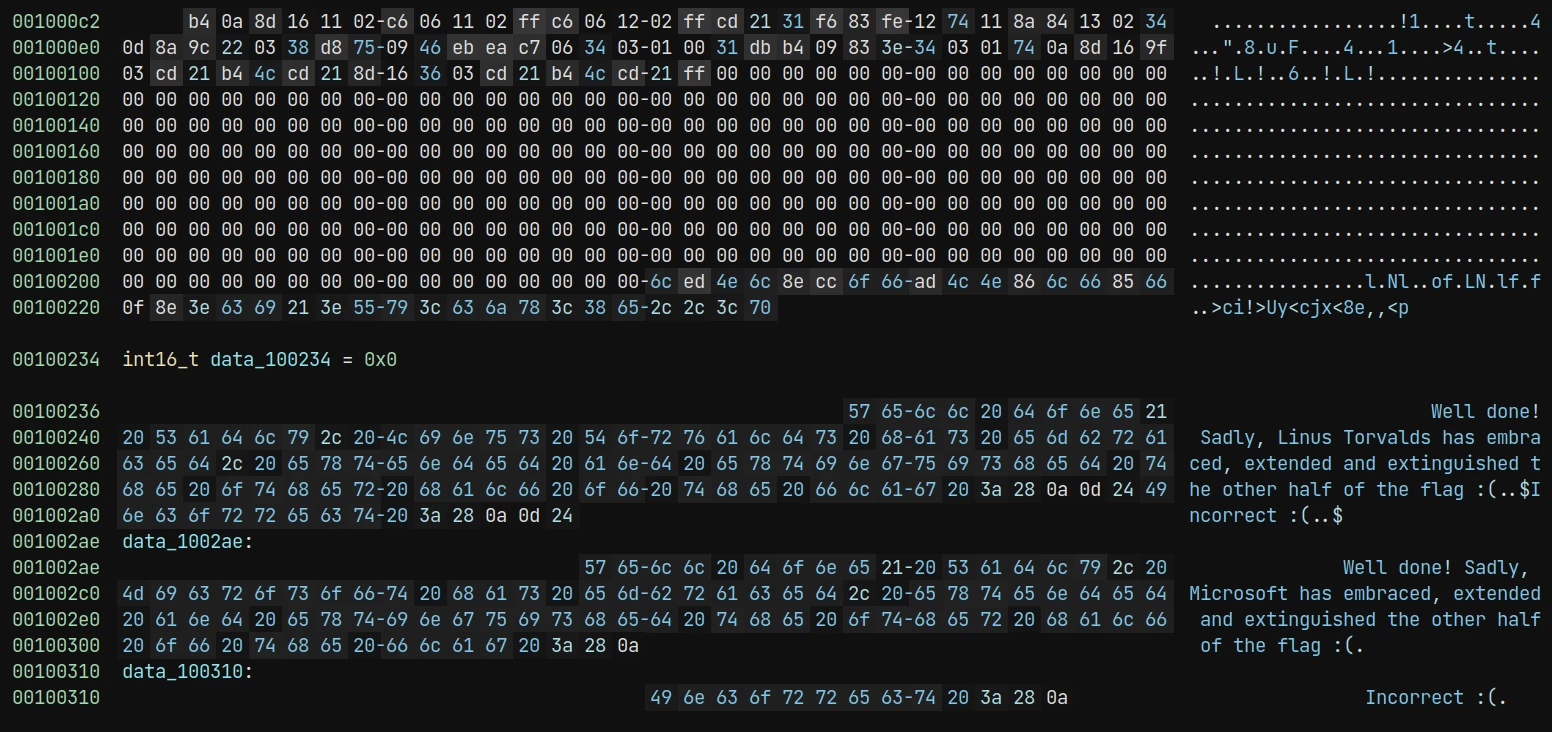
Binary Ninja screenshot2

There are two parts of data string. One of them doesn’t have any cross reference and the end of line is also different. Maybe the author want us to run the binary on Windows? However, I failed to run it on my Windows 11 powershell 7.2.6.

From the first part of flag corctf{3mbr4c3,3xt, we can guess the first three letter of the second part of flag is 3nd. We can further guess the second part of flag is just an xor with the ciphertext. And we flagged!

But why? The author won’t make a naive guess rev challenge. Here, the magic is this binary is also a runnable one under 16-bit DOS System.Try to run with an emulator DosBox or emu2.

$ emu2 m3l.exe 
123
Incorrect :(

Emu2 has an great feature debug option which can show executed CPU instructions. However, we need a small modifiction. The default configuration is write debug output to a file. That’s inconvenient. We can change output to stderr. Change init_debug() in emu2/src/dbg.c to listing below.

void init_debug(const char *base)
{
    if(getenv(ENV_DBG_NAME))
        base = getenv(ENV_DBG_NAME);
    if(getenv(ENV_DBG_OPT))
    {
        // Parse debug types:
        const char *spec = getenv(ENV_DBG_OPT);
        for(int i = 0; i < debug_MAX; i++)
        {
            if(strstr(spec, debug_names[i])) {
                if (i == 0) {
                    debug_files[i] = stderr;
                } else {
                    debug_files[i] = open_log_file(base, debug_names[i]);
                }
            }
        }
    }
}

And run.

$ EMU2_DEBUG="cpu" ./emu2 m3l.exe
AX=0000 BX=0000 CX=00FF DX=0087 SP=FFFE BP=091C SI=0100 DI=FFFE DS=0087 ES=0087 SS=0087 CS=0087 IP=0100 NV UP EI PL NZ NA PO NC 0087:0100 7F45             JG      0147
AX=0000 BX=0000 CX=00FF DX=0087 SP=FFFE BP=091C SI=0100 DI=FFFE DS=0087 ES=0087 SS=0087 CS=0087 IP=0147 NV UP EI PL NZ NA PO NC 0087:0147 EB79             JMP     01C2
AX=0000 BX=0000 CX=00FF DX=0087 SP=FFFE BP=091C SI=0100 DI=FFFE DS=0087 ES=0087 SS=0087 CS=0087 IP=01C2 NV UP EI PL NZ NA PO NC 0087:01C2 B40A             MOV     AH,0A
AX=0A00 BX=0000 CX=00FF DX=0087 SP=FFFE BP=091C SI=0100 DI=FFFE DS=0087 ES=0087 SS=0087 CS=0087 IP=01C4 NV UP EI PL NZ NA PO NC 0087:01C4 8D161102         LEA     DX,[0211]
AX=0A00 BX=0000 CX=00FF DX=0211 SP=FFFE BP=091C SI=0100 DI=FFFE DS=0087 ES=0087 SS=0087 CS=0087 IP=01C8 NV UP EI PL NZ NA PO NC 0087:01C8 C6061102FF       MOV     BYTE PTR [0211],FF
AX=0A00 BX=0000 CX=00FF DX=0211 SP=FFFE BP=091C SI=0100 DI=FFFE DS=0087 ES=0087 SS=0087 CS=0087 IP=01CD NV UP EI PL NZ NA PO NC 0087:01CD C6061202FF       MOV     BYTE PTR [0212],FF
AX=0A00 BX=0000 CX=00FF DX=0211 SP=FFFE BP=091C SI=0100 DI=FFFE DS=0087 ES=0087 SS=0087 CS=0087 IP=01D2 NV UP EI PL NZ NA PO NC 0087:01D2 CD21             INT     21

Here the magic is to use ELF magic as a trampoline. 0x7F45 is JG 0x47 in x86_16 assembly. The program can jump to x86_16 assembly and do xor there. Wow amzing!

hidE

#!/usr/local/bin/python
import random
import time
import math
import binascii
from Crypto.Util.number import *

p, q = getPrime(512), getPrime(512)
n = p * q
phi = (p - 1) * (q - 1)

flag = open('./flag.txt').read().encode()

random.seed(int(time.time()))

def encrypt(msg):
    e = random.randint(1, n)
    while math.gcd(e, phi) != 1:
        e = random.randint(1, n)
    pt = bytes_to_long(msg)
    ct = pow(pt, e, n)
    return binascii.hexlify(long_to_bytes(ct)).decode()


def main():
    print('Secure Encryption Service')
    print('Your modulus is:', n)
    while True:
        print('Options')
        print('-------')
        print('(1) Encrypt flag')
        print('(2) Encrypt message')
        print('(3) Quit')
        x = input('Choose an option: ')
        if x not in '123':
            print('Unrecognized option.')
            exit()
        elif x == '1':
            print('Here is your encrypted flag:', encrypt(flag))
        elif x == '2':
            msg = input('Enter your message in hex: ')
            print('Here is your encrypted message:', encrypt(binascii.unhexlify(msg)))
        elif x == '3':
            print('Bye')
            exit()

if __name__ == '__main__':
    main()

The intended solution of this challenge is to set local random seed as the remote one and do a common modulo attack. I think the hardest part is to guess the random seed of the server. As the latency is non-negligible, I cannot even reproduce others’ writeup. The idea is simple, but hard to find a perfect environment.

CorCTF2022 WriteUp#

tadpole#

luckyguess#

exchanged#

Microsoft ❤️ Linux#

hidE#